Gebäudetechnik, Energie und Nachhaltigkeit – Aufgaben
Dieses Aufgabengebiet wurde erstellt von Martin Brillinger.
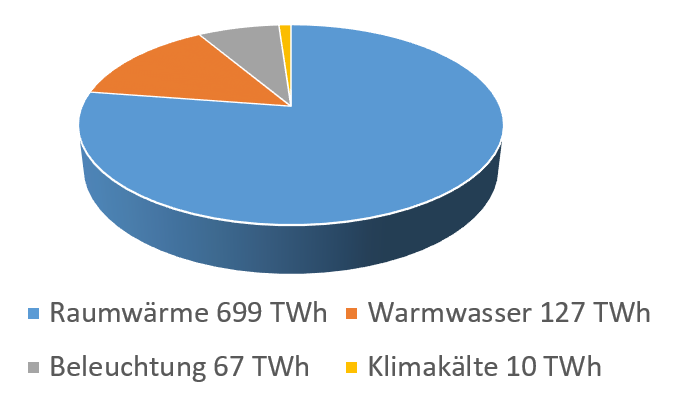
Grafik: Eigene Darstellung. Quelle der Angaben: Deutsche Energie-Agentur (dena, 2019): dena-GEBÄUDEREPORT KOMPAKT 2019 „Statistiken und Analysen zur Energieeffizienz im Gebäudebestand“, S. 19, online verfügbar unter: https://www.dena.de/newsroom/publikationsdetailansicht/pub/broschuere-dena-gebaeudereport-kompakt-2019
Den größten Teil des Energieverbrauchs bei Gebäuden macht der Anteil für den Heizwärmebedarf aus (vgl. Abb. 1), der wiederum durch die Gebäudeform und die Wärmedämmung der Gebäudeaußenflächen maßgeblich beeinflusst wird. In der ersten Aufgabe soll gezeigt werden, wie der Außenwandaufbau den Wärmedurchgang und damit den Heizwärmebedarf beeinflusst, in der zweiten Aufgabe soll der Zusammenhang zwischen der Gebäudeform und der Energieeffizienz verdeutlicht werden. In der dritten Aufgabe wird gezeigt, wie bestehende Gebäude mit Hilfe einer Wärmebildkamera wärmetechnisch analysiert werden können. Alle drei Aufgabenstellungen werden von den Absolvent*innen des Studienganges Smart Building Engineering and Management in deren Berufspraxis bearbeitet und dementsprechend während des Studiums eingeübt.
Das Quellen- und Literaturverzeichnis zu dieser Seite finden Sie hier.
Aufgabe 1 von 4
WÄRMEDURCHGANG DURCH AUSSENWÄNDE
Die konstruktive Zusammensetzung von Bauteilen der Gebäudehülle ist ein entscheidendes Kriterium für den Energieverbrauch von Gebäuden. Die Absolvent*innen des Studienganges Smart Building Engineering and Management können die Energieeffizienz von Bauteilen analysieren und optimieren. Dafür lässt sich der Wärmedurchgang durch einen festen Körper – z.B. eine Außenwand – mit der Berechnung des Wärmedurchgangskoeffizienten (U-Wert) bestimmen. Dieser gibt den Wärmestrom (Wärmeenergie pro Zeiteinheit) für 1 m² eines ebenen Bauteils bei 1 Kelvin Temperaturunterschied zwischen der Innen- und Außenseite des Bauteils an.
Der U-Wert wird durch die Dicke der Bauteilschichten (\(d_i\)) und deren Wärmeleitfähigkeit ( \(λ_i\)) bestimmt. Außerdem gehen die Wärmestrahlung und die Konvektion an den Oberflächen der Bauteile mit dem äußeren Wärmeübergangswiderstand (\(R_{se}\)) und dem inneren Wärmeübergangswiderstand (\(R_{si}\)) in die Berechnungen ein. Je höher der U-Wert eines Bauteils, desto größer ist der Wärmedurchgang bzw. je geringer der U-Wert desto geringer ist der Wärmedurchgang. Ein Bauteil mit einem geringen U-Wert hat also eine gute Wärmedämmung.
Mit untenstehender Formel lässt sich der Wärmedurchgangskoeffizient näherungsweise berechnen. Dabei werden stationäre Verhältnisse vorausgesetzt, d.h. es wird angenommen, dass die Temperaturen auf beiden Seiten des zu berechnenden Bauteils konstant sind. Der Wärmedurchgangswiderstand \(R_T\) ist der Kehrwert des Wärmedurchgangskoeffizienten.
\(U=\frac{1}{R_T} =\frac{1}{R_{se}+\frac{d_1}{λ_1} +\frac{d_2}{λ_2} …+R_{si}}\) \([W/m²K] \)
mit
\(U\): Wärmedurchgangskoeffizient \([W/m^2 K]\), \([Ws/sm^2 K]\)
\(R_T\): Wärmedurchgangswiderstand \([m^2 K/W]\)
\(R_{se}\): äußerer Wärmeübergangswiderstand \([m^2 K/W]\), bei Außenwänden \(0,04\ m^2 K/W\)
\(d_i\): Schichtdicke der Schicht Nummer \(i \ [m]\)
\(λ_i\): spezifische Wärmeleitfähigkeit dieser Schicht \([W/mK]\)
\(R_{si}\): innerer Wärmeübergangswiderstand \([m^2 K/W]\), bei Außenwänden \(0,13\ m^2 K/W\)

Grafik: Eigene Darstellung
|
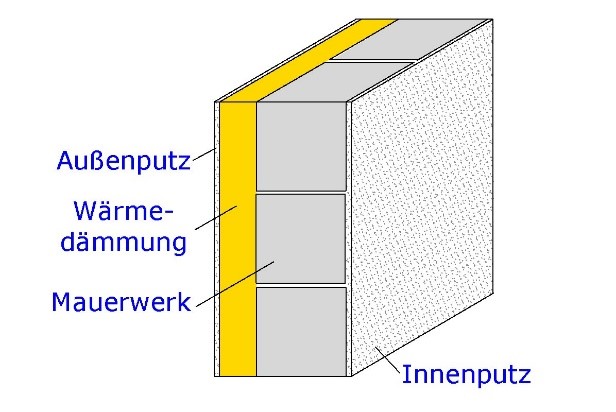
Grafik: Eigene Darstellung
|
|
Aufbau Außenwand 1
|
Aufbau Außenwand 2
|
Berechnen Sie anhand der obenstehenden Formel den Wärmedurchgangskoeffizient für die Außenwand 1! Welches Ergebnis stimmt?
auswählen
Wärmedurchgangskoeffizient Außenwand 1:
\(U=\frac{1}{R_T} =\frac{1}{0,04\ \frac{m^2 K} {W}+\frac{0,015\ m}{0,38\ \frac{W} {mK}}+ \frac{0,365\ m}{0,34\ \frac{W} {mK}}+\frac{0,015\ m}{0,70\ \frac{W} {mK}}+0,13 \frac{m^2 K} {W}} = \frac{1}{0,304\ \frac{m^2 K} {W}} = 0,77\ \frac{W} {m^2K} \).






