Grundausbildung – Beweis durch Induktion
Eine Aufgabe der Mathematik ist es, Strukturen und Zusammenhänge zuerst zu erkennen, dann formal zu beschreiben und schließlich auf ihre logische Konsistenz zu überprüfen. Ein schlüssiger Beweis geht in der Regel weit über bloßes Nachrechnen hinaus. Eine wichtige Technik, mit der eine unendliche Anzahl von Aussagen in endlich vielen Schritten verifiziert werden kann, ist der Induktionsbeweis.
Grafik: Jörg Zintl
Das Quellen- und Literaturverzeichnis zu dieser Seite finden Sie hier.
Aufgabe 1 von 4
Eine Polynomfunktion ist eine Funktion \(f (X)\) mit einer Variablen \(X\) aus den reellen Zahlen, die von der Form
\(f (x) = a_nX^n + a_{n−1} X^{n −1} + . . . + a_1X + a_0\)
ist, wobei die Koeffizienten \(a_0, a_1, . . . , a_n\)fest gewählte reelle Zahlen sind. Ist \(a_n\) nicht Null, dann heißt \(n\geq0\) der Grad von \(f \).
Problem: Beweisen Sie, dass eine Polynomfunktion \(f\) vom Grad \(n \geq1\) höchstens \(n\) Nullstellen besitzt.
Wir versuchen, uns den Beweis dieser bekannten Aussage schrittweise zu erarbeiten. Ein guter Anfang ist es, anhand von Beispielen eine Intuition für das Problem zu bekommen. Zur Hilfe können Sie sich Beispiele zu den Fragen auf einem Blatt Papier aufmalen.
Vervollständigen Sie die folgenden Aussagen.
a) Eine Polynomfunktion von Grad 1 hat mindestens und höchstens Nullstelle(n).
b) Eine Polynomfunktion vom Grad 2 hat mindestens und höchstens Nullstelle(n).
c) Eine Polynomfunktion vom Grad 3 hat mindestens und höchstens Nullstelle(n).
d) Eine Polynomfunktion vom Grad 4 hat mindestens und höchstens Nullstelle(n).
Erklärung zur Lösung der gesamten Aufgabe
Zu a)
Eine Polynomfunktion \(f(x)=a_1 x + a_0\) von Grad 1 beschreibt eine Gerade mit Steigung \(a_1 \neq 0\). Sie schneidet die x-Achse in genau einem Punkt.
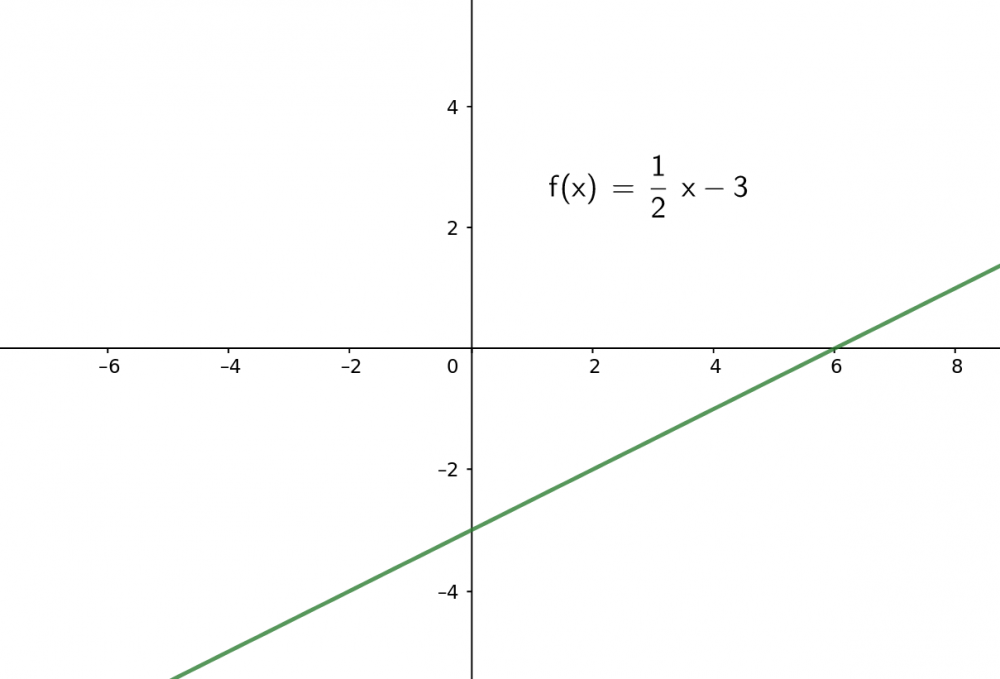
Zu b)
Eine Polynomfunktion \(f(x)=a_2 x^2 + a_1 x + a_0\) von Grad 2 beschreibt eine Parabel (oder ihre Spiegelung an der horizontalen x-Achse). Hier einige Beispiele für typische Graphen:
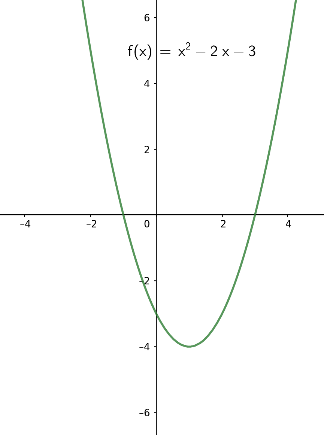
|
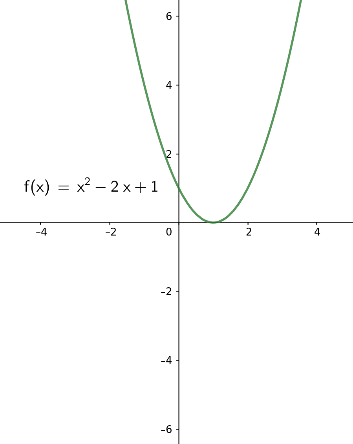
|
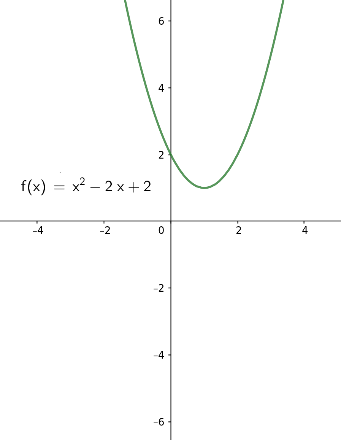
|
Zu c)
Die Graphen von Polynomfunktionen \(f(x)= a_3 x^3 + a_2 x^2 + a_1 x + a_0\) von Grad 3 sehen (bis auf Spiegelung an der horizontalen x-Achse) typischerweise so aus wie in den folgenden Bildern. Beachten Sie, dass die Vorzeichen der Funktionswerte für sehr große und für sehr kleine Werte \(x\) verschieden sind.
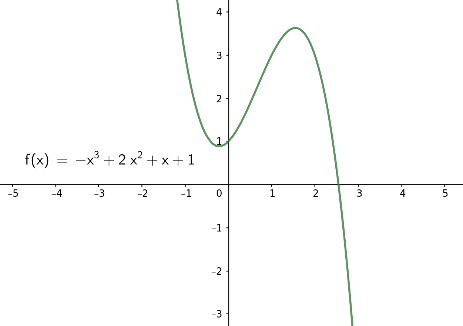
|
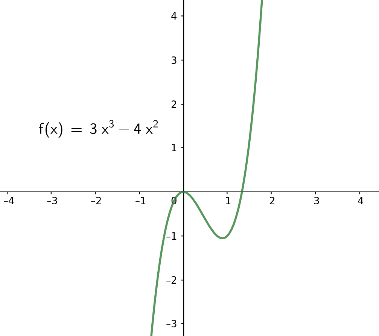
|

|
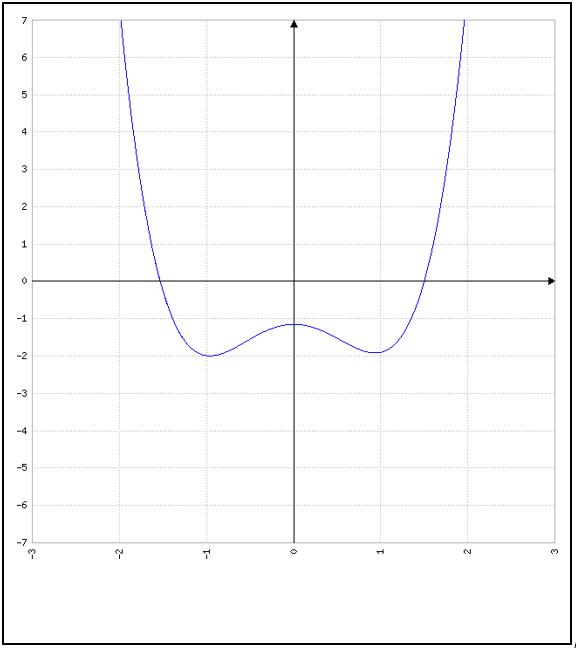
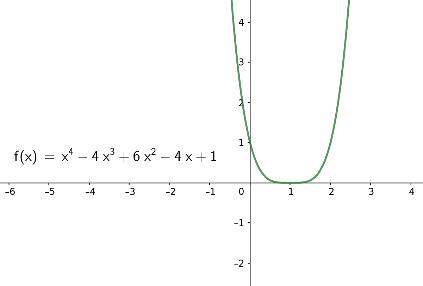
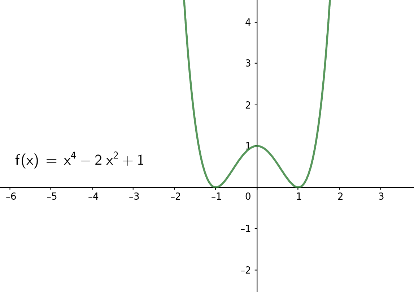
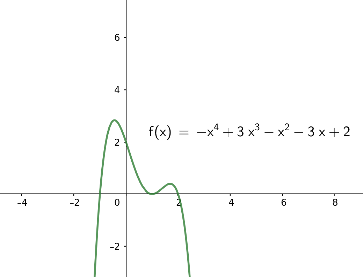
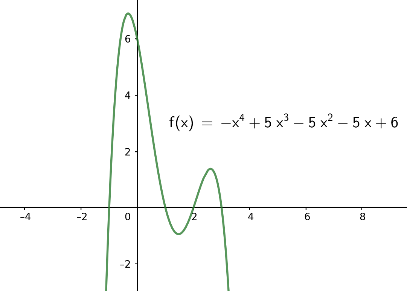
Zu d)
Die Graphen von Polynomfunktionen \(f(x)= a_4 x^4 + a_3 x^3 + a_2 x^2 + a_1 x + a_0\) von Grad 4 sehen (bis auf Spiegelung an der horizontalen x-Achse) typischerweise so aus wie in den folgenden Bildern. Beachten Sie, dass die Vorzeichen der Funktionswerte für sehr große und für sehr kleine Werte \(x\) gleich sind.
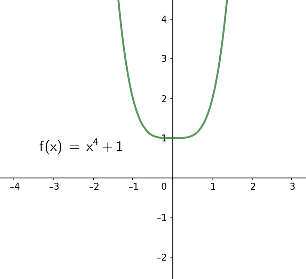
|
|
|
|
|
