Mathematik – Lineare Gleichungssysteme
Dieses Aufgabengebiet wurde erstellt von Thomas Westermann.[1]
Das Quellen- und Literaturverzeichnis zu dieser Seite finden Sie hier.
Aufgabe 1 von 1
DIE BESCHREIBUNG ELEKTRISCHER NETZWERKE BEI GLEICHSTRÖMEN
Lineare Gleichungssysteme (LGS) spielen in Theorie und Anwendungen eine sehr wichtige Rolle. In dieser Aufgabe führen wir am Beispiel eines elektrischen Netzwerkes eine Methode ein, mit der beliebige LGS gelöst werden können: den Gauß-Algorithmus. Gegeben ist das in Abb. 1 angezeigte elektrische Netzwerk mit den Widerständen \(R_1=1\Omega \,,R_2=5\Omega \,,R_3=3\Omega\) . Diesem Netzwerk werden zwei Gleichströme \(I_A=1A\) und \(I_B=2A\) zugeführt. Gesucht sind die Einzelströme \(I_1, I_2, I_3.\)
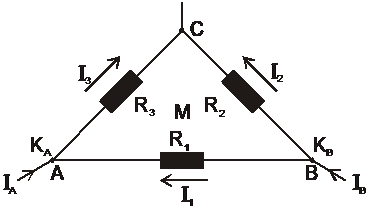
Quelle: Westermann 2012: 26 / Darstellung leicht modifiziert
Um die Modellgleichungen zu erhalten, wenden Sie die Kirchhoffschen Gesetze an: Der Knotensatz besagt, dass die Summe der in einem Knoten zu- und abfließenden Ströme gleich Null ist. Der Maschensatz besagt, dass in einer Masche die Summe aller Spannungen Null ergibt.
Anwenden der Knoten- und Maschenregel
Bei diesem Beispiel gilt für den Knoten \(K_A,\) dass \(I_3\) zu- und \(I_A, I_1\) abfließen
\((K_A):\quad I_3=I_A+I_1;\)
für den Knoten \(K_B,\) dass \(I_B\) zu- und \(I_1, I_2\) abfließen
\((K_B):\quad I_B=I_1+I_2.\)
Für die Masche mit angegebenen Stromrichtungen gilt, dass der Spannungsabfall über \(R_2\) gleich der Summe der Spannungsabfälle über \(R_1\) und \(R_3\) ist:
\((M):\quad R_1I_1+R_3I_3=R_2I_2.\)
Dies ergibt ein System von 3 Gleichungen für die Einzelströme \(I_1, I_2, I_3.\)
Führen Sie so lange Substitutionen durch bis Sie jeweils nur eine Gleichung für eine Unbekannten erhalten.
\(\begin{array}{rrrrrrrr} & & & & & & & \\ G_1:\,\,\, & 1I_1 & - & 5I_2 & + & 3I_3 & = & 0 \\ G_2:\,\,\, & -1I_1 & & & + & 1I_3 & = & 1 \\ G_3:\,\,\, & 1I_1 & + & 1I_2 & & & = & 2 \end{array} \qquad \qquad \qquad \qquad \qquad \qquad \begin{array}{rrr|rr} I_1 & I_2 & I_3 & r.S. \\ \hline 1 & -5 & 3 & 0 \\ -1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 2 \end{array} \)
Dieses System wird gelöst, indem die Variable \(I_1\) aus Gleichungen \(G_2\) und \(G_3\) eliminiert wird. Dazu bildet man die Summe aus Gleichung \(G_1\) und \(G_2\) bzw. die Differenz aus Gleichung \(G_1\) und \(G_3\) :
\(\begin{array}{l} \\ G_1^{\prime }=G_1: \\ G_2^{\prime }=G_1+G_2: \\ G_3^{\prime }=G_1-G_3: \end{array} \; \begin{array}{rrrrrrr} & & & & & & \\ 1I_1 & - & 5I_2 & + & 3I_3 & = & 0 \\ & - & 5I_2 & + & 4I_3 & = & 1 \\ & - & 6I_2 & + & 3I_3 & = & -2 \end{array} \; \qquad \qquad \qquad \qquad \begin{array}{rrr|rr} I_1 & I_2 & I_3 & r.S. \\ \hline 1 & -5 & 3 & 0 \\ 0 & -5 & 4 & 1 \\ 0 & -6 & 3 & -2 \end{array} \)
Anschließend nehmen wir Gleichung \(G_2^{^{\prime }}\) und \(G_3^{^{\prime }}\) und eliminieren die Variable \(I_2\) aus \(G_3^{^{\prime }}.\)
Dazu addieren wir das 6-fache von Gleichung \(G_2^{^{\prime }}\) zum (\(-5\))-fachen von Gleichung \(G_3^{^{\prime }}:\)
\(\begin{array}{rrrrr} -30I_2 & + & 24I_3 & = & 6 \\ 30I_2 & - & 15I_3 & = & 10 \\ \hline & & 9I_3 & = & 16 \end{array} \)
Damit erhalten wir schließlich
\(\begin{array}{l} \\ G_1^{^{\prime \prime }}=G_1: \\ G_2^{^{\prime \prime }}=G_2^{\prime }: \\ G_3^{^{\prime \prime }}=6G_2^{^{\prime }}-5G_3^{^{\prime }}: \end{array} \; \begin{array}{rrrrrrr} & & & & & & \\ 1I_1 & - & 5I_2 & + & 3I_3 & = & 0 \\ & - & 5I_2 & + & 4I_3 & = & 1 \\ & & & & 9I_3 & = & 16 \end{array} \qquad \qquad \qquad \qquad \begin{array}{rrr|rr} I_1 & I_2 & I_3 & r.S. \\ \hline 1 & -5 & 3 & 0 \\ 0 & -5 & 4 & 1 \\ 0 & 0 & 9 & 16 \end{array} \)
Lösen Sie nun die Gleichungen für die zugehörigen Ströme.
Aus Gleichung \(G_3^{^{\prime \prime }}\) folgt
\(9I_3=16\Rightarrow I_3=\frac{16}9.\)
Eingesetzt in Gleichung \(G_2^{^{\prime \prime }}\) folgt
\(-5I_2+4\cdot \frac{16}9=1\Rightarrow I_2=\frac{11}9.\)
Beide Ergebnisse in Gleichung \(G_1^{^{\prime \prime }}\) eingesetzt liefert
\(I_1-5\cdot \frac{11}9+3\cdot \frac{16}9=0\Rightarrow I_1=\frac 79.\)
Damit sind die Teilströme \(I_1,I_2,I_3\) berechnet.
