Mathematik
– Beispielaufgaben
Das Quellen- und Literaturverzeichnis zu dieser Seite finden Sie hier.
Aufgabe 1 von 10
BIG SALE
Oft ist es sinnvoller Aufgaben durch Überlegung und Verständnis zu lösen, als ein auswendiggelerntes Rechenverfahren anzuwenden.

Grafik: alex80 / Pixabay License / Quelle: Pixabay
Herr Müller kauft für 37,00 € ein. An der Kasse erhält er einen Rabatt von 19%. Wie viel muss er jetzt bezahlen?
28,91 €
31,98 €
29,98 €
29,97 €
Sollten Sie ausschließlich durch eine Rechnung auf die Lösung gekommen sein, bedenken Sie: Von 19% fehlt nicht ‚sonderlich viel‘ zu 20%.
Aufgabe 2 von 10
FLÄCHENVERGLEICH
Gerade die Berechnung von Flächen erfolgt oft durch unüberlegtes Anwenden von auswendig gelernten Formeln. Lässt sich die folgende Aufgabe auch anders lösen?
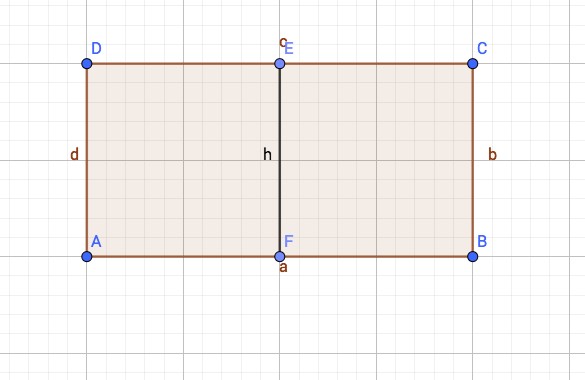
Grafik: Klaus-Peter Eichler (PH Schwäbisch Gmünd)
|
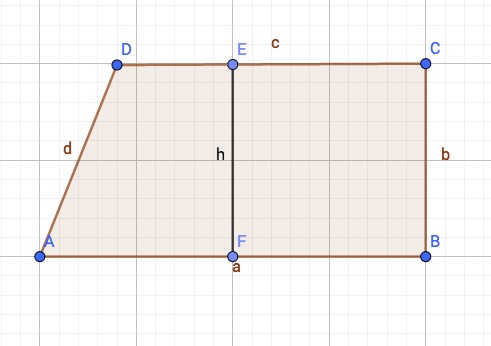
Grafik: Klaus-Peter Eichler (PH Schwäbisch Gmünd)
|
|
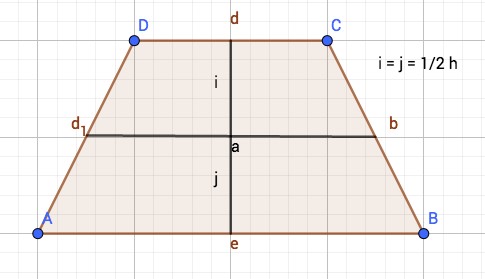
Grafik: Klaus-Peter Eichler (PH Schwäbisch Gmünd) |
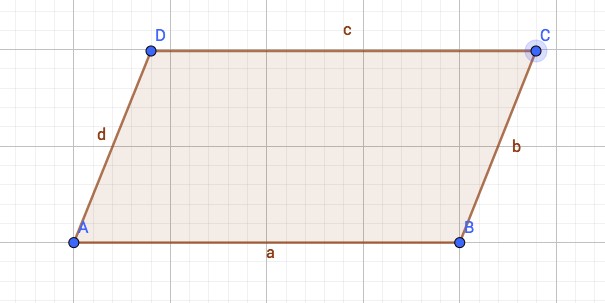
Grafik: Klaus-Peter Eichler (PH Schwäbisch Gmünd) |
Wählen Sie aus, welche Aussage richtig und welche falsch ist.
F1 = F2
Alle Flächen sind gleich groß.
F1 = F3 = F4
F1 = F4
F1 = F3
Abschneiden und an anderer Stelle ‚ankleben‘ können Ihre Schülerinnen und Schüler nur dann mental, also im Kopf, leisten, wenn den Kindern zuvor die Möglichkeit geboten wurde, dies tatsächlich durchzuführen.
Aufgabe 3 von 10
GEBROCHEN RECHNEN
Um Schülerlösungen schnell interpretieren zu können, müssen Sie als Mathematiklehrkraft Lösungswege schnell durchschauen. Dann können Sie Schülerinnen und Schüler gezielt unterstützen.
Hier lief etwas schief. Was genau?
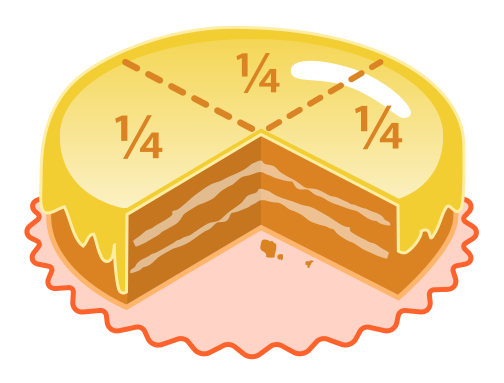
Grafik: Acdx / gemeinfrei / Quelle: Wikimedia Commons
Ordnen Sie den Aufgaben die jeweiligen Fehler zu.
\(\frac{2}{3}\cdot2=\frac{2}{3\cdot2}=\frac{1}{3}\)
\(2\frac{2}{3}\div2=\frac{2}{2}\frac{2}{3\cdot2}=\frac{1}{1}\frac{1}{3}=\frac{1}{3}\)
\(4\frac{2}{3}\div2\frac{1}{3}=4\div2+\frac{2}{3}\div\frac{1}{3}=2+2=4\)
\(5\div2=\frac{5}{1}\div\frac{1}{2}=\frac{5}{1}\cdot\frac{2}{1}=10\)
Die 2 wird nicht als ganze Zahl erkannt.
falsche Umrechnung der gemischten Zahl
ganze Zahl mal ganze Zahl und Bruch mal Bruch
falsche Umrechnung der 2 in einen Bruch
Im Studium lernen Sie nicht nur, die Art von Fehlern zu erkennen, die Schülerinnen und Schülern passieren, sondern eben auch, auf welchen Fehlvorstellungen diese Fehler beruhen. So manche Lösung erweist sich als (für die Lernenden) durchaus schlüssig. Nur wenn Sie durchschauen, welche Fehlvorstellung zu einem Fehler geführt hat, können Sie passend unterstützen.
Aufgabe 4 von 10
LOG ER ODER LOG ER NICHT?
Mathematische Formeln nicht nur als Lösungstool zu verstehen, das man nachschlägt, sondern sie sinnvoll herzuleiten und einzusetzen, ist ein wichtiges Ziel des Mathematikunterrichtes.
Gelingt es Ihnen hier?
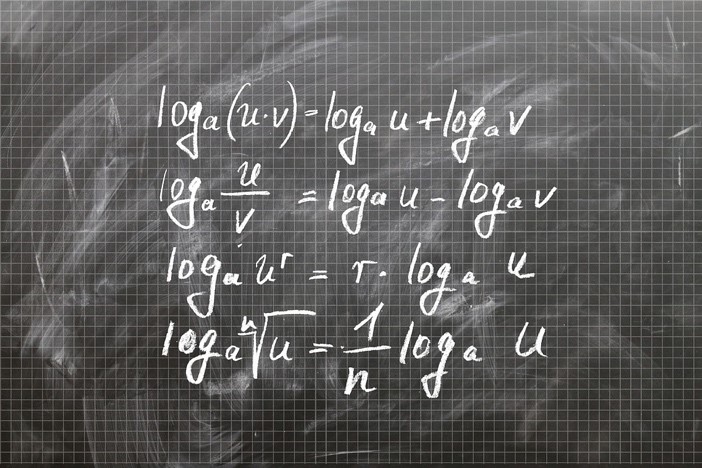
Grafik: geralt / Pixabay License / Quelle: Pixabay
Berechnen Sie: log2 (4 · 8) + log2 (72 : 9). Wie lautet das Ergebnis?
5
3
8
4
10
Aufgabe 5 von 10
MAL ANDERS
Funktionale Zusammenhänge erschließen sich nicht direkt und einfach. Ein möglicher Zugang ist das Nachdenken über proportionale bzw. antiproportionale Zusammenhänge.
„Je mehr Käse, desto mehr Löcher.
Je mehr Löcher, desto weniger Käse.
Ergo: Je mehr Käse, desto weniger Käse.“ (unbekannt)

Foto: Aexas_Fotos / Pixabay License / Quelle: Pixabay
Zwei Maler brauchen für das Streichen von 2m Wand 2 Stunden. Wie viele Meter Wand streichen drei Maler in drei Stunden?
3 m
6 m
4,5 m
nicht lösbar
Im Studium werden Sie sich ausführlich mit dem Funktionsbegriff auseinandersetzen. Beim eben berechneten Beispiel mussten Sie die Anzahl der Maler, getrennt von der Anzahl an Arbeitsstunden und Leistung betrachten. Damit Schülerinnen und Schüler eine Vorstellung davon entwickeln können, wie sich die Änderung von ‚x‘ auf ‚y‘ auswirkt, müssen sie zunächst viele Beispiele durchdenken und, so möglich, erleben, um die Sinnhaftigkeit mathematischen Rechnens begreifen zu können. Mathematik bleibt sonst sinnloses Zahlen hin- und herschieben.
Aufgabe 6 von 10
PRISMA
Wer mathematische Begriffe wie Viereck oder Quader benutzt, verbindet damit oft ganz konkrete Vorstellungen über bestimmte prototypische Vertreter dieser geometrischen Figuren. Dabei geraten manche Merkmale, die die jeweilige geometrische Figur definieren, aus dem Blickfeld.
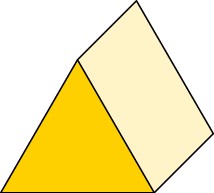
Grafik: Klaus-Peter Eichler (PH Schwäbisch Gmünd)
Welche Aussage trifft auf ein Prisma zu?
Ein Prisma hat immer eine dreieckige Fläche.
Ein Gegenbeispiel wäre ein Würfel.
Alle Würfel sind Prismen.
Das Volumen eines Prismas ist das Produkt aus der Grundfläche und seiner Höhe.
Quader sind keine Prismen.
Ein Prisma ist ein geometrischer Körper der durch Parallelverschiebung eines ebenen Vielecks entlang einer nicht in dieser Ebene liegenden Geraden im Raum entsteht. Ein Quader entsteht durch Parallelverschiebung eines Rechteckes und ist daher ein Prisma.
Ein Prisma hat immer genau zwei zueinander kongruente Flächen.
Manchmal – wie beim Würfel – sind es mehr als zwei zueinander kongruente Flächen.
Begriffe einzuführen und zu festigen ist ein zentraler Bestandteil des Mathematikunterrichts. Welche Bilder vor dem inneren Auge erscheinen, wenn Sie einen Begriff (hier: Prisma) hören, hängt maßgeblich davon ab, wie Mathematiklehrkräfte die Begriffe einführen. Wer unter Prisma nur ein Dreiecksprisma versteht, wird sich bei dieser Aufgabe schwergetan haben.
Aufgabe 7 von 10
MUSTER AUS GEOMETRISCHEN FIGUREN
„Der Wissenschaftler findet seine Belohnung in dem, was Poincaré die Freude am Verstehen nennt, nicht in den Anwendungsmöglichkeiten seiner Erfindung.“ (Albert Einstein)
Kindern diese Freude zu vermitteln, ist Ihre Aufgabe als Lehrerin bzw. als Lehrer. Das können Sie schon mit vergleichsweise einfachen Aufgaben erreichen, indem Sie den Kindern durch eigene Überlegungen zum Heureka-Moment verhelfen.
Schon beim Beantworten der Frage, wie viele Vierecke in einem Streifen aus Quadraten zu finden sind, werden viele Kinder nicht zeichnen und zählen, sondern andere Lösungswege finden.
Lösen Sie die unten stehende Aufgabe zunächst, verallgemeinern Sie und überlegen Sie dann, wie Sie Kinder auf dem Weg zur Lösung unterstützen können.
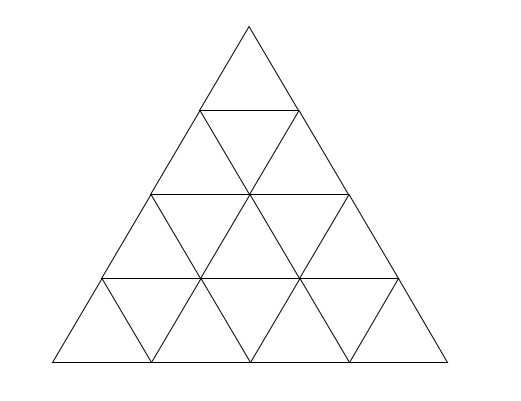
Grafik: Klaus-Peter Eichler (PH Schwäbisch Gmünd) |
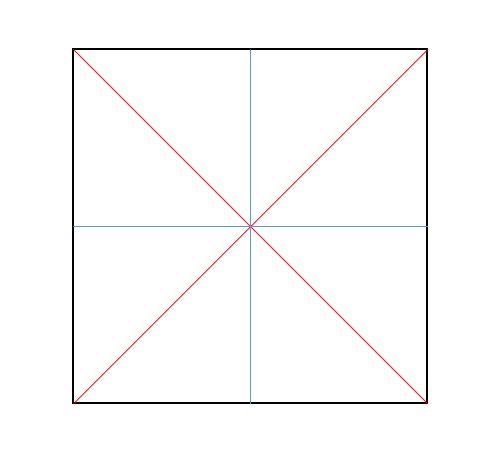
Grafik: Klaus-Peter Eichler (PH Schwäbisch Gmünd) |
|
Hier sind 13 Dreiecke zu sehen. |
Hier sind es 16 Dreiecke. |

Grafik: Klaus-Peter Eichler (PH Schwäbisch Gmünd)
Wie viele Vierecke befinden sich in einem Streifen aus hundert Quadraten?
100
1000
5050
505
10000
Glaubt man die Geschichte, dann hat sich der kleine Carl Friedrich Gauß schon als Grundschüler mit dieser Art Aufgaben auseinandergesetzt. Der Streifen aus hundert Quadraten steht für die Summe aus den ersten 100 Zahlen. Ein Quadrat ist ein Rechteck. Zwei Quadrate sind 3 (1+2). Vier Quadrate schon 6 (1+2+3) usw.
Aufgabe 8 von 10
RECHENTREPPEN
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
6 + 9 = 15
9 + 15 = 24
15 + 24 = 39
Solche ‚Rechentreppen‘ mit drei Stufen kann sich jeder selbst ausdenken.
Ida hat sich eine Rechentreppe ausgedacht, verrät jedoch die Startzahlen nicht. Sie nennt nur ihr Ergebnis: 100.
__ + __ = __
__ + __ = __
__ + __ = 100
Wie viele verschiedene Möglichkeiten gibt es, zu Idas Rechentreppe passende Startzahlen zu wählen?
5
17
16
25
3
Gute Aufgaben für den Unterricht motivieren alle und wirken dadurch differenzierend. Sie nehmen also alle Kinder im Klassenraum mit und verlieren nicht leistungsschwächere oder unterfordern leistungsstarke Kinder.
In diesem Fall können es beispielsweise alle Kinder leisten, eine eigene Rechentreppe zu ‚bauen‘. Leistungsstärkere beantworten die Frage, die Ihnen gestellt wurde. Haben Sie alle 17 Möglichkeiten gefunden?
Aufgabe 9 von 10
SPIROLATERALE
„Das entscheidende Kriterium ist Schönheit; für hässliche Mathematik ist auf dieser Welt kein beständiger Platz.“ (Godfrey Hardy)
Eine Zeichenaufgabe, die bereits von Kindern in Klasse 1 bewältigt werden kann, ist das Zeichnen von sogenannten Spirolateralen nach vorgegebenen Zahlen. Eine Zahlenfolge wie beispielsweise 1 – 2 – 3 – 4 – 5 wird vorgegeben. Auf Quadratgitterpapier wird gezeichnet. Dabei wird immer ‚in Fahrtrichtung‘ rechts abgebogen.

Grafik: Klaus-Peter Eichler (PH Schwäbisch Gmünd)
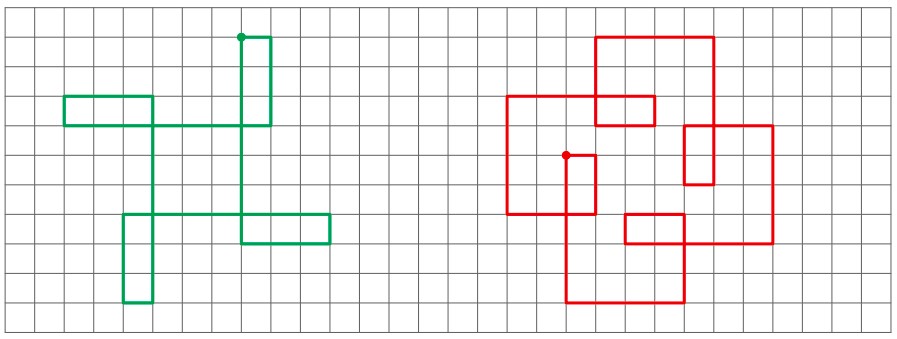
Grafik: Klaus-Peter Eichler (PH Schwäbisch Gmünd)
Zeichnen Sie (mindestens) die folgenden Spirolaterale:
1-2-3
2-4-3-2
4-2-2-3-2
Welche der folgenden Aussagen sind richtig? Warum ist das so? Finden Sie einen Beweis.
Alle Spirolaterale schließen sich.
Zeichnen Sie das Spirolateral 2-2-10-2
Spirolaterale mit vier Zahlen schließen sich immer.
Zeichnen Sie das Spirolateral 2-2-10-2
Spirolaterale mit fünf Zahlen schließen sich immer.
Spirolaterale mit drei Zahlen schließen sich immer.
Verallgemeinern wir: das Spirolateral a-b-c
Schauen Sie sich in der Tabelle an, wie weit Sie jeweils nach rechts, unten, links und oben gegangen sind.
|
Nach rechts |
Nach unten |
Nach links |
Nach oben |
|
a |
b |
c |
a |
|
b |
c |
a |
b |
|
c |
a |
b |
c |
Aufgabe 10 von 10
ARITHMETIK UND GEOMETRIE
„Wer die Geometrie begreift, vermag in dieser Welt alles zu verstehen.“ (Galileo Galilei)
Durch die gezielte Verbindung von Arithmetik und Geometrie werden mathematische Sachverhalte sichtbar, die allein durch Formeln ausgedrückt oft abstrakt erscheinen.
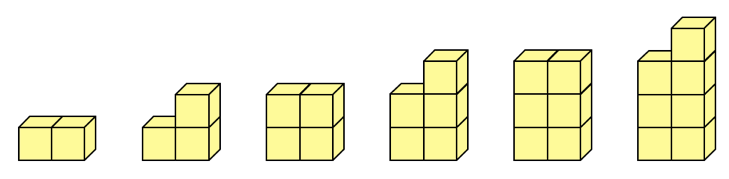
Grafik: Klaus-Peter Eichler (PH Schwäbisch Gmünd)
Baut man ‚Zweiertürme‘ wird rasch ‚einsichtig‘ welche Zahlen gerade und welche ungerade sind.

Grafik: Klaus-Peter Eichler (PH Schwäbisch Gmünd)
In Abb. 16 wird deutlich, dass die Summe zweier ungerader Zahlen eine gerade Zahl ist.
Was lässt sich an den folgenden Würfelgebäuden erkennen?

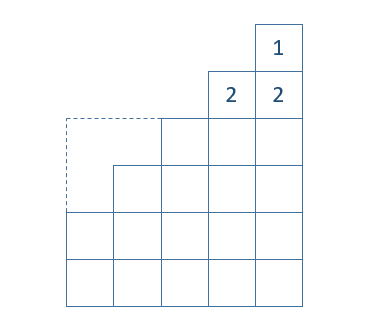
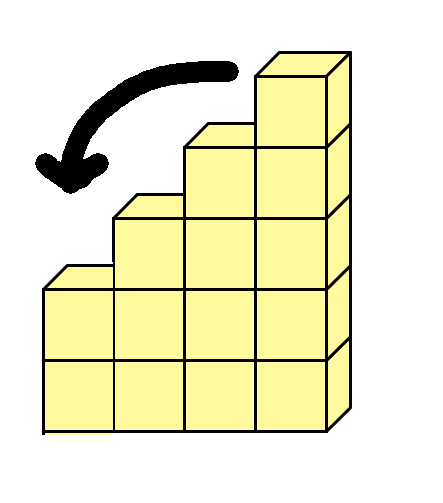
Addiert man aufeinanderfolgende ungerade Zahlen, so ist die Summe immer eine Quadratzahl.
Die Summe von fünf aufeinanderfolgenden Zahlen ist immer durch 5 teilbar.
Die Summe von vier aufeinanderfolgenden Zahlen ist nie ein Vielfaches von 4.
